Go back to the list of projects
Revising ternary ALU design
30/09/2019

This article is part of my series of projects around Ternary Computing and Processor Design. Click here to see the list of projects of this series.

As promised, more of my Ternary Computer project. In the previous article on the topic, I promised I would explain how I designed the PCB to build the ALU. However, before doing that, I wanted to count how many gates I would need for the 3-trit ALU. A while ago, I wrote an article on the design of a ternary ALU. I also said in that article that we could spare gates by tweaking the design slightly.

Small spoiler altert for the next article, but here are the PCBs I designed and the number of CD4007 chips on each :

As you can see, some PCBs combine multiple gates, either because I had extra space or because some gates include other gates, which is the case of the NSUM gate which requires a NCONS gate.

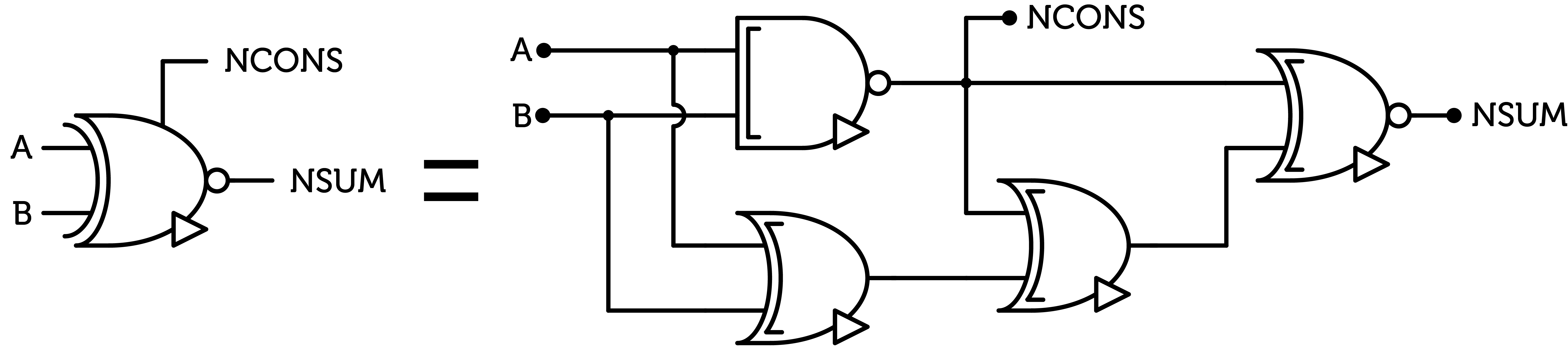
NSUM with NCONS secondary output

But first, let's take the original design and count the cost in chips and the PCBs needed by climbing the layers of abstraction. First, the fundamental gate of the ALU is the SUM gate. Using the formula and diagram described in the first article I made about ternary logic, each SUM gate costs 11 CMOS pairs, thus 11 CD4007 chips. Then to build a half-adder, we need a SUM gate and a CONS gate for a total of 14 chips. Then the full-adder requires two half-adders and a ANY gate, 31 chips. The first digit of the ALU is a single half adder (because there is no incoming carry trit), 14 chips, and the last digits is two SUM gates (no output carry trit, even though it is often the case that the last carry bit in a binary ALU is stored in a flag for branching instructions and the ability to do calculations with multiple words), 22 chips ; the rest are full-adders. For a $$n$$-trit ALU ($$n\geq 2$$), the total cost of the ALU (not including the sign controller required for subtraction) is $$(14+31(n-2)+22) = (31n-26)$$ chips. For a 3-trit ALU, that amounts to 67 chips.

As stated earlier, we can spare one CONS gate, per half-adder by using the NCONS gate in the SUM gate and adding just a NOT gate. That saves 2 chips per half-adder. The new total cost is $$(27n-20)$$ chips, 61 chips for a 3-trit ALU (-6).

Another economy comes from something else. In the first article, I mentioned the following formulas. ££{A ⊠ B} = \overline{A} ⊠ \overline{B} ££ ££{A ⊞ B} = \overline{A} ⊞ \overline{B} ££ ££{A \otimes B} = \overline{A} \otimes \overline{B} ££ ££{A \oplus B} = \overline{A} \oplus \overline{B} ££ And this is huge. If we invert both inputs of a SUM gate, the output is unchanged. But why invert the inputs ? Adding NOT gates will increase the cost ! Well, yes, obviously. The trick is to use inverted gates before the input, and since those inverted gates are usually cheaper, we can save chips. This is simpler to understand with diagrams :

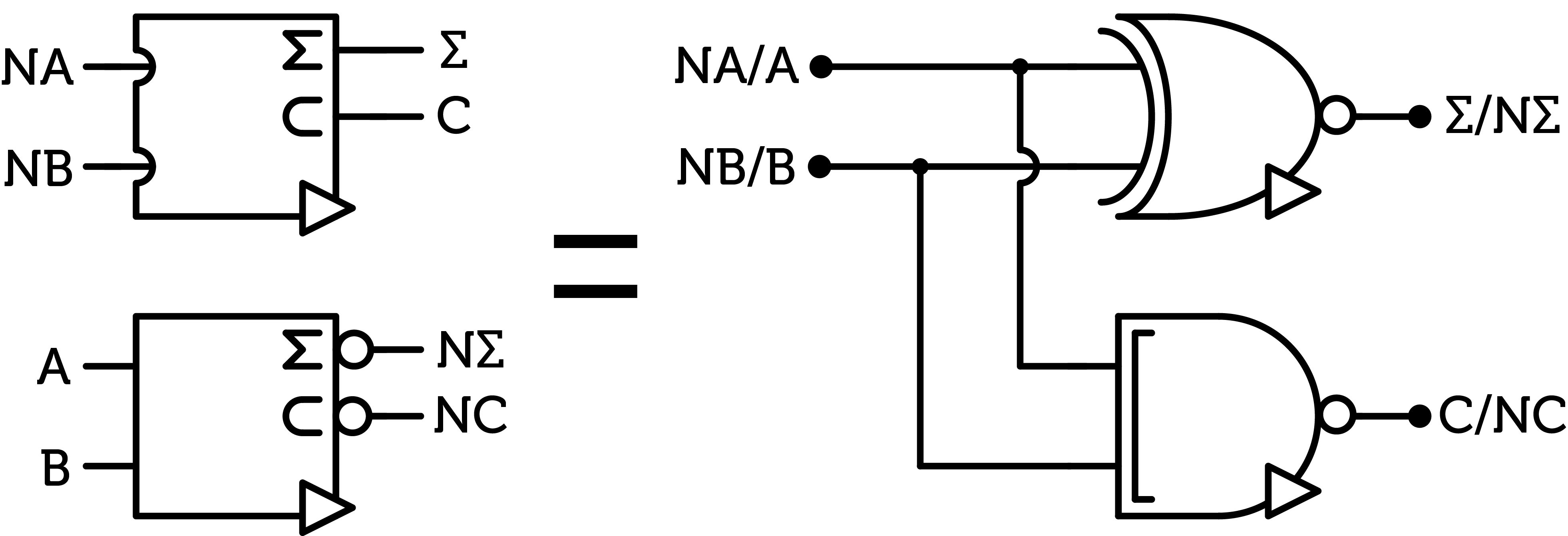
N-half-adder

Here I defined an alternative half-adder. I created two symbols and here is why. The circle on the output still means that the output is inverted compared to the default gate (here the half-adder). The round cup on the input is supposed to indicate an inverter should be present on the input ; that is, to get the behavior of the default gate, we have to invert this input. Here, the two symbols, taken with the labels, are the same : to get the behavior of the default half-adder, we can either invert both output or both inputs. This is a direct consequence of the formulas listed above.

Using this N-half-adder, we can create a N-full-adder :

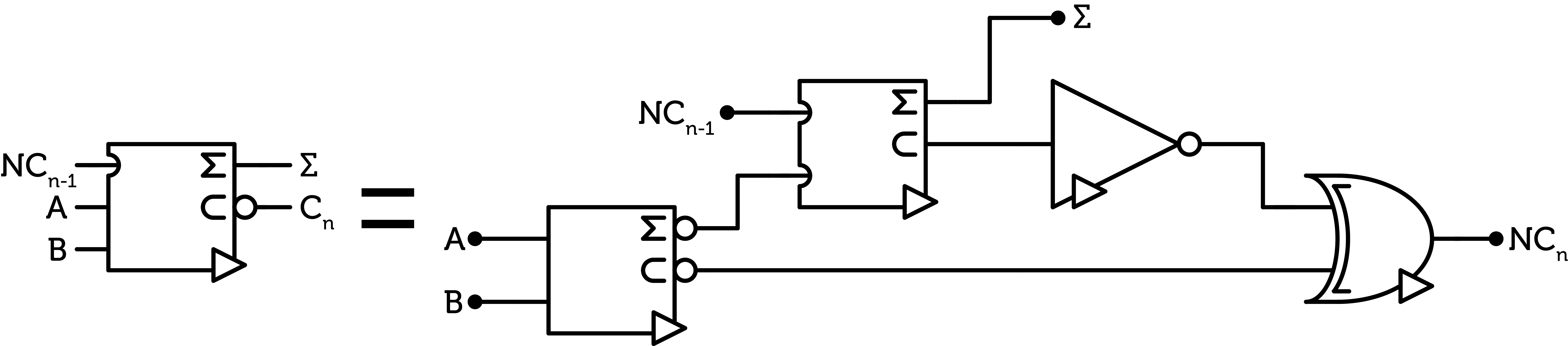
N-full-adder

Again, let me remind you that both N-half-adders on this diagram correspond to the same internal circuitry described above. However, on the bottom one, we feed the original A and B signals, so we get the inverted sum and inverted carry of A and B. While on the top one, we feed in the inverted incoming carry and the inverted sum from the first N-half-adder, so we get the un-inverted final sum and the un-inverted carry. So, one carry is inverted and the other is not. To combine the two carries, we have to invert one and thus add a NOT gate. Then, as we want the inverted total carry, we have to use a NANY which is more expensive than the ANY.

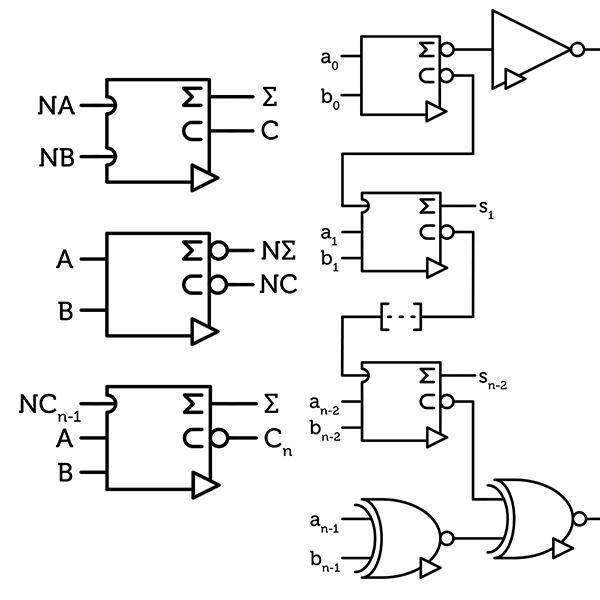
Finally, we can build our full ALU again. As expected, the first and last digits are also different.

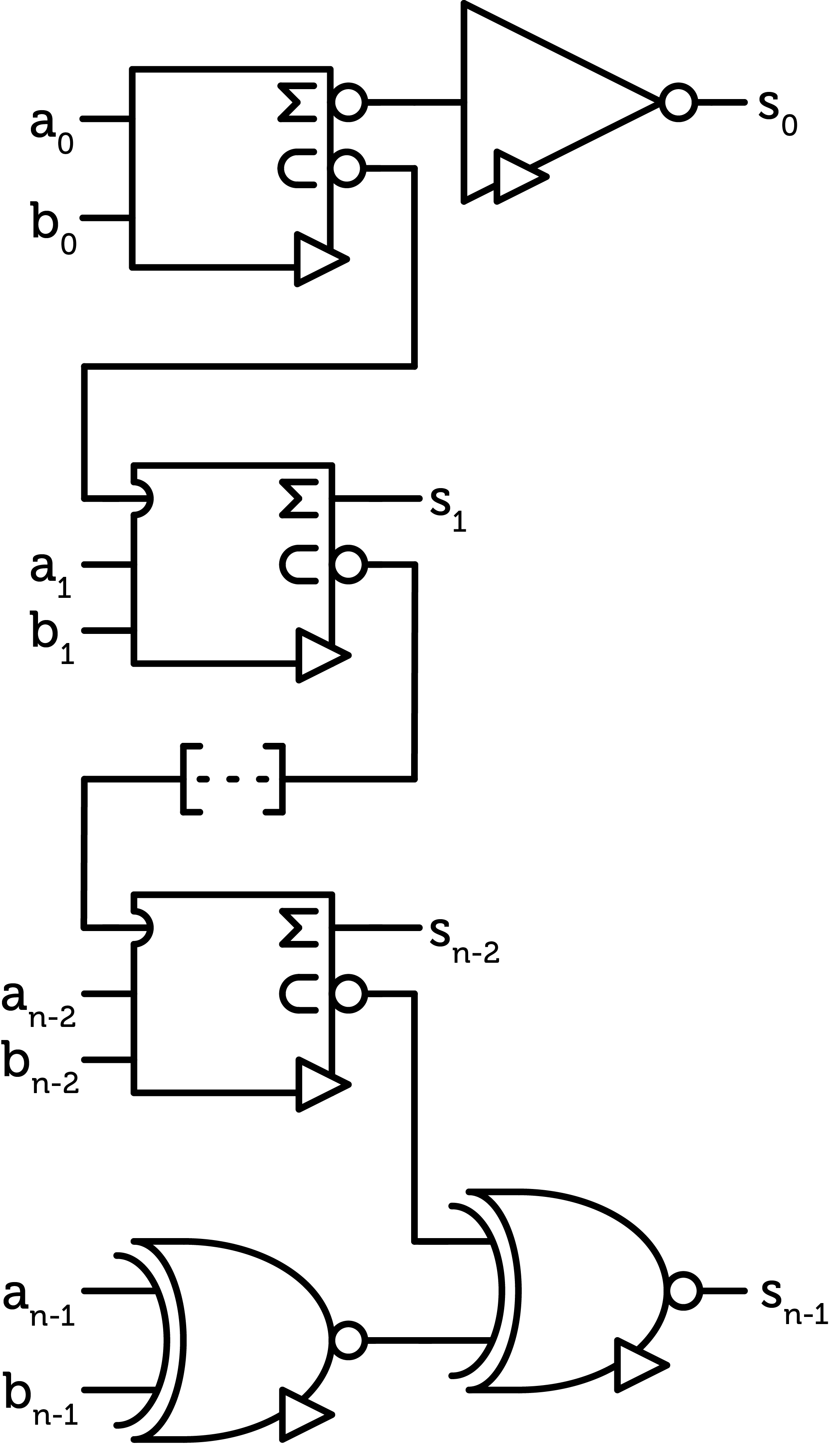
New adder chain

Now let's calculate the new cost. With those modifications, the N-half-adder costs 10 chips (-2), the N-full-adder 24 chips (-2), the first digit 11 chips (-1) and the last digit 21 chips (-1). The total and final cost is $$(24n-16)$$ chips, 56 chips for a 3-trit ALU (-5).

Finally, let's count the PCBs required. Each N-half-adder is 1 NSUM+NCONS. A N-full-adder is 2 NSUM+NCONS, 1 NANY and 1 full 2xNOT (one NOT for the ANY and one for the carry). The first digit is 1 NSUM+NCONS and 0.5 2xNOT. The last digit is 2 NSUM+NCONS (only the NSUM are used). For a 3-trit ALU, this amounts to 5 NSUM+NCONS, 1 NANY and 1.5 2xNOT.

Beside an economy of chips and PCBs, the optimizations also reduce the number of CMOS pairs the signal has to propagate through, and thus increases the maximum frequency of the processor. We will take a look at this much later.

That was a lot of new circuitry ! I could have done a mistake, so I checked the whole behavior of the circuit, once on paper and once with TelociDesi, the piece of software I developed last year to simulate whole ternary circuits. I can confirm everything works perfectly. Here are the circuits on TelociDesi :

N-half-adder

N-full-adder

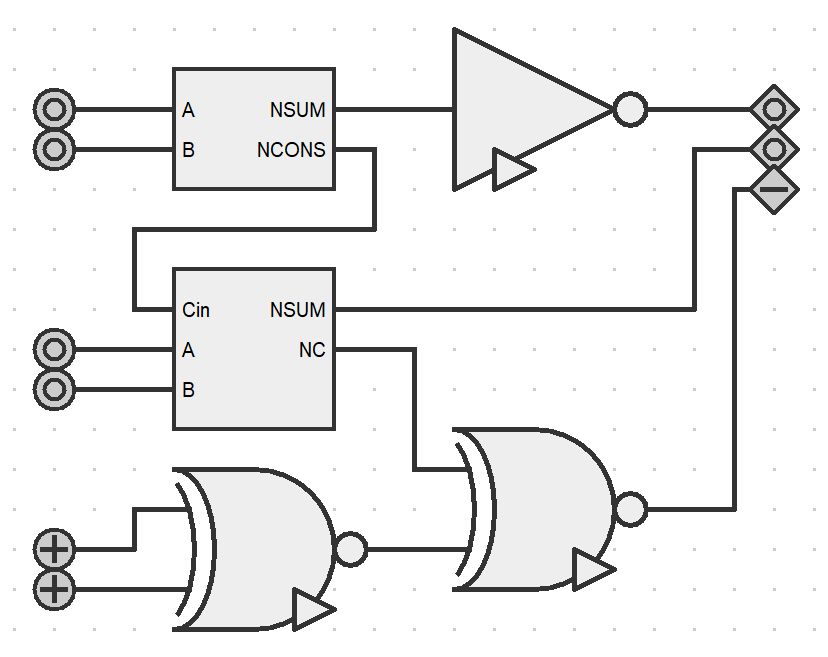
3-trit ALU

This article is part of my series of projects around Ternary Computing and Processor Design. Click here to see the list of projects of this series.

Go back to the list of projects